Cours 3 : Eviews

CHAPITRE IV : ESTIMATION D’UN MODELE LINEAIRE

1. Spécification du modèle et hypothèses

Nous essayons d’estimer une fonction de consommation sous linéaire comme suit :

Nos variables sont tous logués. Nous avons Lcons comme variable dépendante et Lpib, Lipc et Lgt comme explicative. a_0 représente la constante et e_t l’erreur.

Pour valider notre modèle linéaire apres estimation, on doit vérifier les hypothèses suivantes sur les résidus :

H1 : Les erreurs sont de moyenne nulle

H2 : La variance des erreurs est constante (Homoscédasticité)

H3 : Les erreurs sont indépendants

H4 : Les erreurs suivent une loi normale

2.  Estimation du modèle

Pour estimer notre modèle, on a deux possibilités :

• sélectionner, dans le menu principal, Quick/Estimate Equation….Dans la fenêtre qui s’affiche, on tape l’équation en commençant par la variable endogène suivie d’une constante et des variables explicatives.
• sélectionner les variables qui interviennent dans l’équation en commençant par la variable endogène (LCONS), à faire ensuite un clic droit et à sélectionner Open as Equation.
• On pourra loguer les variables directement dans la fenêtre qui s’affiche.

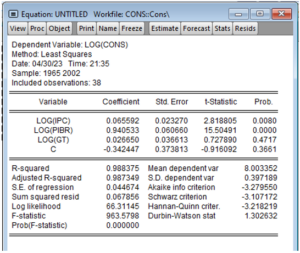
On obtient le tableau ci contre.

Ce tableau présente les principales caractéristiques de la régression.

• La première partie du tableau nous présente les variables, les coefficients estimés et leurs significativités à travers la p-value.
• La seconde partie montre les caractéristiques globale du modèle.

Interprétation des résultats de la régression :

• La partie basse du tableau nous montre que notre modèle est globalement significatif (p-value associé à la F-stat : 0,0000). Aussi, le R2-adjusté associé au modèle est de 0,987. Ce qui veut dire la variance expliquée par notre modèle est de 98,7% ce qui est assez grand.
• La partie haute du tableau nous renseigne sur les variables. On note que seul les variables significatives au seuil de 5% sont Lpibr et Lipc. Donc on peut interpréter les coefficients associés.

Tests de diagnostique des résidus

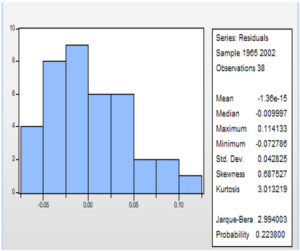
• Test de normalité des résidus (Test de Jarque-Bera : Pour réaliser ce test, cliquer sur  View ensuite « Residual diagnostic » et choisir « Histogram – Normality test ».
• L’hypothèse nulle : Normalité des résidus
• La p-value associé à la statistique de Jarque-Bera est 0,22 > 5%. Donc on accepte l’hypothèse nulle de normalité des résidus.

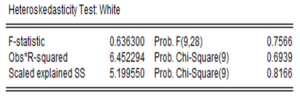
• Test d’hétéroscédasticité(Test de White) : Pour réaliser ce test, cliquer sur  View ensuite « Residual diagnostic » et choisir « Heteroscedasticity test» puis white.
• L’hypothèse nulle : Homoscédasticité
• La p-value associé au test est 0,69 > 5%. Donc on ne peut rejeter l’hypothèse nulle d’homoscédasticité des résidus

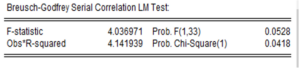
• Test d’autocorrélation(Test de Breusch et Godfrey) : Pour réaliser ce test, cliquer sur  View ensuite « Residual diagnostic » et choisir « Serial Correlation LM Test» puis choisir le nombre de retards.
• L’hypothèse nulle : Absence d’autocorrélation
• La statistique de test de Breusch-Godfrey reporte une probabilité de 0.041 < 5%. Ces valeurs nous amènent à rejeter l’hypothèse nulle d’absence d’autocorrélation d’ordre un des erreurs.

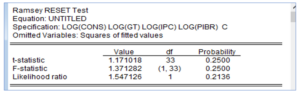
• Test de spécification(Test de Ramsey) : Pour réaliser ce test, cliquer sur  View ensuite « Stability test» et choisir « Ramsey RESET test» puis choisir le nombre de retards.
• L’hypothèse nulle : Absence d’autocorrélation
• La probabilité critique de la statistique de test indique qu’il n’y a pas d’erreur de spécification dans l’équation estimée.