Cours 4 : STATA

CHAPITRE V : LA REGRESSION LINEAIRE

Définition et hypothèses

• La régression linéaire est une des techniques les plus simple pour expliquer une variable quantitative continue en fonction d’autres variables.

Mathématiquement on cherche à estimer le vecteur de paramètre β  dans l’équation :  y=Xβ+ ε

Où y est le vecteur des observations de la variable à expliquer, X la matrice des variables explicatives et ε le vecteur des erreurs.

• La commande Stata qui permet de réaliser une régression linéaire est regress.
• Syntaxe : regress y var1 var2 … varn où y est la variable à expliquer et Var1, var2, … ,varn sont les variables explicatives.

Pour valider notre modèle linéaire après estimation, on doit vérifier les hypothèses suivantes sur les résidus :

H1 : Les erreurs sont de moyenne nulle

H2 : La variance des erreurs est constante (Homoscédasticité)

H3 : Les erreurs sont indépendants

H4 : Les erreurs suivent une loi normale

Cas pratique

• En guise d’illustration pour cette partie, supposons qu’on veut expliquer la consommation (CONS) des ménages par le pib par habitant noté PIBR et l’indice des prix à la consommation noté IPC.

On a le modèle :  CONS = αPIBR+ βIPC+ ε

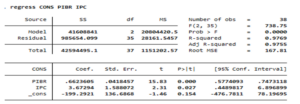
Les résultats de commande regress sont présentés dans le tableau précédent.

Dans la partie haute du tableau, on retrouve le R2 et le R2 ajusté au nombre d’explicatives. Ils donnent la le pourcentage de variance expliquée par notre modèle (0,97 ou 97%). On y retrouve également la statistique de Fisher et la p-value associée (0,0000) qui montre que notre modèle est globalement significatif.

La seconde partie donnes la liste des coefficients estimés et leurs valeurs et p-value. Une variable est significative au seuil de 5% si la p-value associé à l’estimation de son coefficient est inférieure à 0,05. Dans notre cas, les 2 variables sont significatives.

Tests Post estimation

Test après estimation : Apres estimation de notre modèle, il est important d’effectuer des tests afin de valider le modèle. Il s’agit du test d’endogénéité, du test de normalité des résidus, du test d’homoscédasticité et du test de multi colinéarité.

• Test d’endogénéité : La présence de variable endogène conduira à des estimations biaisées. Pour corriger cet effet, on utilise généralement des variables instrumentales. Dans le cas de notre exemple, on fait le test de Durbon et Wu Hausman: estat endogenous

• Test de multi colinéarité : Pour vérifier la multi colinéarité on peut utiliser le vif. La syntaxe est : estat vif

Aussi, on peut avoir une idée grâce à la matrice de corrélation en utilisant pwcorr. Lorsqu’on a deux variables explicatives significativement corrélées, on garde un seul des deux ou bien on fait la moyenne des deux.

• Test de normalité des résidus : On peut utiliser le test de Shapiro Wilk vu précédemment sur les résidus de la régression.

Predict residual, resid # Pour créer la variable « residual » vecteur des résidus

 swilk residual  #Fait le test de normalité sur le vecteur de résidu

• Test d’homoscédasticité : On peut utiliser le test de Breush pagan donné par la commande hettest. L’hypothèse nulle est l’homogénéité des résidus.

Syntaxe : estat hettest